(i)     elementary particle.

(ii)     antiparticle of a lepton.

The electron is a lepton and its antiparticle is the positron. The following reaction can take place between an electron and positron.

\[{e^ - } + {e^ + } \to \gamma  + \gamma \]

Sketch the Feynman diagram for this reaction and identify on your diagram any virtual particles.

(i)     quark structure of the \({\pi ^ + }\) meson.

(ii)     reason why the following reaction does not occur.

\[{p^ + } + {p^ + } \to {p^ + } + {\pi ^ + }\]

(i)     a particle that cannot be made from any smaller constituents/particles;

(ii) has the same rest mass (and spin) as the lepton but opposite charge (and opposite lepton number);

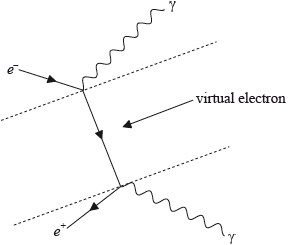
Award [1] for each correct section of the diagram.

\({e^ - }\) correct direction \(\gamma \);

\({e^ + }\) correct direction and \(\gamma \);

virtual electron/positron;

Accept all three time orderings.

(i)     \({\rm{u\bar d}}\) / up and anti-down;

(ii)     baryon number is not conserved / quarks are not conserved;

Part (a) was often correct.

The Feynman diagrams rarely showed the virtual particle.

A significant number of candidates had a good understanding of quark structure.

Explain why the virtual particle in this Feynman diagram must be a weak interaction exchange particle.

A student claims that the \({{\text{K}}^ + }\) is produced in neutron decays according to the reaction \({\text{n}} \to {{\text{K}}^ + } + {{\text{e}}^ - }\). State one reason why this claim is false.

the decay does not conserve strangeness;

and only the weak interaction violates strangeness conservation;

or

a neutrino is produced in this decay;

neutrinos interact only via the weak interaction;

does not conserve baryon/quark/lepton number;

A lambda baryon \({\Lambda ^0}\) is composed of the three quarks uds. Show that the charge is 0 and the strangeness is \( - 1\).

Discuss, with reference to strangeness and baryon number, why this proposal is feasible.

Strangeness:

Baryon number:

Another interaction is

\[{\Lambda ^0} \to p + {\pi ^ - }\]

In this interaction strangeness is found not to be conserved. Deduce the nature of this interaction.

\( + \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = 0\) for charge;

any particle containing a strange quark has strangeness of \( - 1\);

strangeness:

the \(p\) has a strangeness of 0;

the \({K^ - }\) particle has a strangeness of \( - 1\);

baryon number:

lambda and protons are baryons each having a baryon number of \( + 1\);

the \({K^ - }\) meson has a baryon number of 0;

only during the weak interaction strangeness is not conserved (therefore it is a weak interaction);

Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii). SL candidates showed more difficulty with (b)(iii), often using an incorrect approach.

Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii). SL candidates showed more difficulty with (b)(iii), often using an incorrect approach.

Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii). SL candidates showed more difficulty with (b)(iii), often using an incorrect approach.

Aluminium-26 decays into an isotope of magnesium (Mg) by \({\beta ^ + }\) decay.

\[_{{\text{13}}}^{{\text{26}}}{\text{Al}} \to _{\text{Y}}^{\text{X}}{\text{Mg}} + {\beta ^ + } + {\text{Z}}\]

Identify X, Y and Z in this nuclear decay process.

X:

Y:

Z:

Explain why the beta particles emitted from the aluminium-26 have a continuous range of energies.

State what is meant by half-life.

A meteorite which has just fallen to Earth has an activity of 36.8 Bq. A second meteorite of the same mass, which arrived some time ago, has an activity of 11.2 Bq. Determine, in years, the time since the second meteorite arrived on Earth.

X: 26 and Y: 12; (both needed for [1])

Z: v/neutrino;

Do not allow the antineutrino.

total energy released is fixed;

neutrino carries some of this energy;

(leaving the beta particle with a range of energies)

the time taken for half the radioactive nuclides to decay / the time taken for the activity to decrease to half its initial value;

Do not allow reference to change in weight.

\(\lambda  = \left( {\frac{{\ln 2}}{{7.2 \times {{10}^5}}} = } \right){\text{ }}9.63 \times {10^{ - 7}}\);

\(11.2 = 36.8{e^{ - (9.63 \times {{10}^{ - 7}})t}}\);

\(t = 1.24 \times {10^6}{\text{ (yr)}}\);

This was generally well answered, although a significant minority insisted that nuclear half-life is defined by a loss of mass.

This was generally well answered, although a significant minority insisted that nuclear half-life is defined by a loss of mass.

This was generally well answered, although a significant minority insisted that nuclear half-life is defined by a loss of mass.

This was generally well answered, although a significant minority insisted that nuclear half-life is defined by a loss of mass.

Identify the type of fundamental interactions associated with the exchange particles in the table.

State why \({\pi ^ + }\) mesons are not considered to be elementary particles.

Identify the exchange particle associated with this decay.

Deduce that this decay conserves baryon number.

electromagnetic;

strong;

they are composed of more than one quark;

\({W^ + }\);

u has a baryon number of \(\frac{1}{3}\) and \({\rm{\bar d}}\) has a baryon number of \( - \frac{1}{3}\) ;

\({\mu ^ + }\) and \({v_\mu }\) both have a baryon number of 0;

(a)(i) was well answered.

(a)(ii) was well answered.

Most answers to (b)(ii) used quark baryon numbers of 1 etc, not \(\frac{1}{3}\).

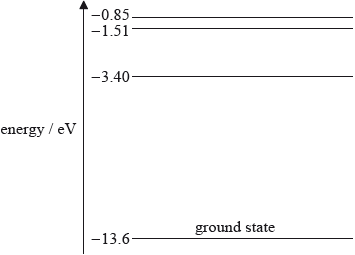
Explain how atomic line spectra provide evidence for the existence of discrete electron energy levels in atoms.

(i)     Calculate the wavelength of the photon that will be emitted when an electron moves from the –3.40 eV energy level to the –13.6 eV energy level.

(ii)     State and explain if it is possible for a hydrogen atom in the ground state to absorb a photon with an energy of 12.5 eV.

each line represents a single frequency/wavelength;

which corresponds to a specific photon energy / \(E = hf\);

energy of photon determined by energy change of electrons;

electrons transition between energy levels (so discrete energy levels);

Award [3 max] for reverse argument that discrete energy levels produce line spectra.

(i)     \(\Delta E = [13.6 - 3.40] \times 1.60 \times {10^{ - 19}}{\text{ (}} = 1.63 \times {10^{ - 18}}{\text{ J)}}\);

\(E = \frac{{hc}}{\lambda }\); (accept implicit use of this equation)

\(\lambda  = \frac{{6.63 \times {{10}^{ - 34}} \times 3.00 \times {{10}^8}}}{{1.63 \times {{10}^{ - 18}}}} = 1.22 \times {10^{ - 7}}{\text{ (m)}}\);

Award [3] for a correct bald answer.

(ii)     photon absorbed when its energy is equal to the difference between two energy levels;

so absorption not possible;

In (a) the logical sequence is: line spectra ➡ discrete photon energy ➡ discrete electron transitions ➡ discrete electron energy levels. However, very few were able to sequence their answers in this way. Despite this there were many reasonable answers.

In (i) many correct answers were seen, but there were some answers where the de Broglie formula was mistakenly used. (ii) was poorly answered as few could explain that a 12.5eV photon did not match any of the possible transition energies.

Identify the missing entries in the following nuclear reaction.

\[{}_{11}^{22}{\rm{Na}} \to {}_ \ldots ^{22}{\rm{Ne}} + {}_ \ldots ^0e + {}_0^0 \ldots \]

Define half-life.

Sodium-22 has a decay constant of 0.27 yr^–1.

(i) Calculate, in years, the half-life of sodium-22.

(ii) A sample of sodium-22 has initially 5.0 × 10²³ atoms. Calculate the number of sodium-22 atoms remaining in the sample after 5.0 years.

\({}_{11}^{22}{\rm{Na}} \to {}_{10}^{22}{\rm{Ne}} + {}_{ + 1}^0e + {}_0^0v\)
\({}_{10}^{22}{\rm{Ne}}\);
\({}_{ + 1}^0e\) (accept \({}_ + ^0e\))
\({}_0^0v\); (award [0] for \({}_0^0\bar v\))

time taken for half/50% of the nuclei to decay / activity to drop by half/50%;

(i) \({T_{\frac{1}{2}}} = \frac{{\ln 2}}{\lambda }\);
\(\frac{{0.693}}{{0.27{\rm{y}}{{\rm{r}}^{ - 1}}}}\)=2.6 (years);
Award [2] for a bald correct answer.

(ii) N=5.0 x 10²³ x e^-0.27x5.0;
N=1.3 x 10^23;
Award [2] for a bald correct answer.

Calculate the difference in energy in eV between the energy levels in the hydrogen atom that give rise to the red line in the spectrum.

\(E = \left( {\frac{{hc}}{\lambda } = } \right){\text{ }}3.03 \times {10^{ - 19}}{\text{ J}}\);

\( = 1.90{\text{ eV}}\);

Award [2] for bald correct answer.

The calculation in (b) was often correctly done.

A nucleus of a radioactive isotope of gold (Au-189) emits a neutrino in the decay to a nucleus of an isotope of platinum (Pt).

In the nuclear reaction equation below, state the name of the particle X and identify the nucleon number \(A\) and proton number \(Z\) of the nucleus of the isotope of platinum.

\[_{\;79}^{189}Au \to _Z^APt + X + v\]

X:

A:

Z:

(i)     Calculate the decay constant of Au-189.

(ii)     Determine the activity of the sample after 12.0 min.

X: positron or \({\beta ^ + }\);

A: 189 and Z: 78; (both responses needed)

(i)     \(0.0784{\text{ mi}}{{\text{n}}^{ - 1}}\);

(ii)     recognize to use \(A = {A_0}{e^{ - \lambda t}}\);

\(A = 48.4{\text{ Bq}}\);

Award [2] for bald correct answer.

A surprisingly large number of candidates were unable to correctly identify the products of beta plus decay.

Unit errors were often made in (i) and in (ii) there was often some very strange arithmetic to be seen.

Outline how atomic absorption spectra provide evidence for the quantization of energy states in atoms.

The diagram shows some atomic energy levels of hydrogen.

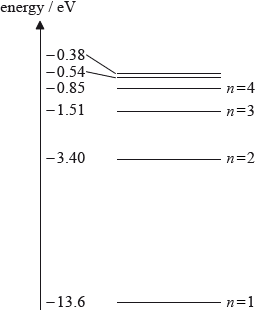
A photon of energy 2.86 eV is emitted from a hydrogen atom. Using the diagram, draw an arrow to indicate the electron transitions that results in the emission of this photon.

an atom will only absorb a photon if the photon energy corresponds to an energy difference between two of its energy states;

the absorption of energy takes places in discrete quantities (quanta);

arrow drawn downwards from \( - 0.54\) level to \( - 3.40\) level;

In (a), candidates rarely described absorption spectra, rather explaining emission spectra. There were very poor explanations of quantized energy states.

(b) was generally well answered, although a common mistake was to have the change in the wrong direction.

The following particle interaction is proposed.

\[p + {\pi ^ - } \to {K^ - } + {\pi ^ + }\]

In this interaction, charge is conserved.

State, in terms of baryon and strangeness conservation, whether the interaction is possible.

baryon (1+ 0→0 + 0) not conserved and strangeness (0 + 0→−1+ 0) not conserved;
so interaction not possible;

Identify the numbers and the particle to complete the decay equation.

State the nature of the \({\beta ^ + }\) particle.

Outline a method for measuring the half-life of an isotope, such as the half-life of carbon-11.

State the law of radioactive decay.

Derive the relationship between the half-life \({T_{\frac{1}{2}}}\) and the decay constant \(\lambda \) , using the law of radioactive decay.

Calculate the number of nuclei of carbon-11 that will produce an activity of \(4.2 \times {10^{20}}{\text{ Bq}}\).

\(\left( {_{\;6}^{11}{\text{C}} \to _{\;5}^{11}{\text{B}} + _{ + 1}^{\;\;0}{\beta ^ + } + v{\text{ (or neutrino)}}} \right)\)

\(_{\;6}^{11}{\text{C}} \to _{\;5}^{11}{\text{B}} + _{ + 1}^{\;\;0}{\beta ^ + }\);

v (or neutrino);

Award [1] for all the correct numbers and [1] for the neutrino.

positron / antielectron / lepton;

measure activity as a function of time;

create a graph of activity with time, and estimate half-life from the graph;

make at least three estimates of half-life from the graph and take mean;

or

measure activity as a function of time;

create a graph of ln(A) with time, find the decay constant \(\lambda \) from the gradient;

estimate the half-life using \({T_{\frac{1}{2}}} = \frac{{\ln 2}}{\lambda }\);

the rate of decay is proportional to the amount of (radioactive) material remaining;

the number of undecayed nuclei at time \(t\) is given by \(N = {N_0}{e^{ - \lambda t}}\), where \({N_0}\) is the number of undecayed nuclei at time \(t = 0\) and \(\lambda \) is the decay constant;

\(\frac{{{N_0}}}{2} = {N_0}{e^{ - {T_{\frac{1}{2}}}}}\);

\(\ln \left( {\frac{1}{2}} \right) =  - \lambda {T_{\frac{1}{2}}}\) so \({T_{\frac{1}{2}}} = \frac{{\ln 2}}{\lambda }\);

\(\lambda  = \frac{{\ln 2}}{{60 \times 20.3}}{\text{ }}( = 5.69 \times {10^{ - 4}}{s^{ - 1}})\);

\(\frac{A}{\lambda } = \frac{{4.2 \times {{10}^{20}}}}{{5.69 \times {{10}^{ - 4}}}} = 7.4 \times {10^{23}}\);

(a)(i) was well answered.

(a)(ii) was well answered.

(b)(i) was poorly answered, with many referring to measurement of the loss of mass of the sample.

(b)(ii) was very poorly answered.

Most did not use the law of radioactive decay, as required in (b)(iii).

(b)(iv) was either very well answered or very poorly answered.

State

(i) what is meant by an elementary particle.

(ii) to which class of elementary particles the electron belongs.

An electron is one of the particles produced in the decay of a free neutron into a proton. An exchange particle is also involved in the decay.

(i) State the name of the exchange particle.

(ii) The weak interaction has a range of the order of 10^–18m. Determine, in GeVc^–2, the order of magnitude of the mass of the exchange particle.

(iii) It is suggested that the exchange particle in the weak interaction arises from the decay of one type of quark into another. With reference to the quark structure of nucleons, state the reason for this suggestion.

(i) particle that has no internal structure/is not made out of any smaller constituents;

(ii) leptons;

(i) intermediate vector boson/W boson;

(ii) \(m = \frac{h}{{4\pi Rc}}\);
\( = \left( {\frac{{6.6 \times {{10}^{ - 34}}}}{{4 \times 3.14 \times {{10}^{ - 18}} \times 3.0 \times {{10}^8}}} = } \right)1.75 \times {10^{ - 25}}{\rm{kg}}\);
\( = \frac{{1.75 \times {{10}^{ - 25}}{c^2}}}{e} = 109{\rm{GeV}}{{\rm{c}}^{ - 2}} \approx 10^2{\rm{GeV}}{{\rm{c}}^{ - 2}}\);

(iii) the neutron quark structure is udd and the proton uud;
a d quark in the neutron changes to a u quark by emitting a W boson;

State what is meant by the term elementary particle.

The strong interaction between two nucleons has a range of about 10^–15 m.

(i) Identify the boson that mediates the strong interaction. 

(ii) Determine the approximate mass of the boson in (b)(i).

particle with no internal structure / cannot be broken down further;

(i) pion/meson/gluon;

(ii) \(m = \frac{h}{{4\pi Rc}}\);

1.8x10^-28(kg);

A nuclide of the isotope potassium-40 \(\left( {{}_{19}^{40}{\rm{K}}} \right)\) decays into a stable nuclide of the isotope
argon-40 \(\left( {{}_{18}^{40}{\rm{Ar}}} \right)\). Identify the particles X and Y in the nuclear equation below.

\[{}_{19}^{40}{\rm{K}} \to {}_{18}^{40}{\rm{Ar + X + Y}}\]

The half-life of potassium-40 is 1.3×10⁹yr. In a particular rock sample it is found that 85 % of the original potassium-40 nuclei have decayed. Determine the age of the rock.

State the quantities that need to be measured in order to determine the half-life of a long-lived isotope such as potassium-40.

neutrino/ν;
positron / e⁺ / \({}_{ + 1}^0{\rm{e}}\) / β⁺;
Award [1 max] for wrongly stating electron and antineutrino. Both needed for the ECF.
Order of answers is not important.

\(\lambda  = \left( {\frac{{\ln 2}}{{1.3 \times {{10}^9}}} = } \right)5.31 \times {10^{ - 10}}{\rm{y}}{{\rm{r}}^{ - 1}}\);
\(0.15 = {{\rm{e}}^{\left[ { - 5.31 \times {{10}^{ - 10}} \times t} \right]}}\);
t=3.6×10⁹yr;
Award [3] for a bald correct answer.

or

(0.5)ⁿ=0.15;
\(n = \frac{{\log \left( {0.15} \right)}}{{\log \left( {0.5} \right)}} = 2.74{\rm{half - lives}}\);
2.74×1.3×10⁹=3.6×10⁹yr;
Award [3] for a bald correct answer.

the count rate/activity of a sample;
the mass/number of atoms in the sample;

Outline a laboratory procedure for producing and observing the atomic absorption spectrum of a gas.

(i) Describe the appearance of an atomic absorption spectrum.

(ii) Explain why the spectrum in (a) provides evidence for quantization of energy in atoms.

The principal energy levels of the hydrogen atom in electronvolt (eV) are given by

\[{E_n} = \frac{{13.6}}{{{n^2}}}\]

where n is a positive integer.

Determine the wavelength of the absorption line that corresponds to an electron transition from the energy level given by n=1 to the level given by n=3.

shine white light through;
a tube of the gas;
then observe with spectroscope/grating/prism;

(i) continuous spectrum crossed by dark lines;

(ii) dark lines formed by the absorption of photons;
the absorbed photons have specific/discreet wavelengths;
indicating discreet differences in energy;
which can only be explained by existence of energy levels;

\(E = 13.6\left[ {\frac{1}{{{1^2}}} - \frac{1}{{{3^2}}}} \right] = 12.1{\rm{eV}}\);
12.1eV=12.1×1.6×10^–19J =\(\frac{{hc}}{\lambda }\);
λ=102nm or 103nm;
Award [3] for a bald correct answer.

State what is meant by an exchange particle.

A meson called the pion was detected in cosmic ray reactions in 1947 by Powell and Occhialini. The pion comes in three possible charge states: π⁺ ,π⁻ and π⁰. The Feynman diagram below represents a possible reaction in which a pion participates.

State and explain whether the meson produced is a π⁺ ,π⁻ or  a π⁰.

a particle that mediates/carries/transmits one of the fundamental forces / a particle that is exchanged between two particles when undergoing one of the fundamental interactions / OWTTE;

π⁺;
from conservation of charge at either vertex, the pion must have charge of +1;

Suggest why the kaon is classified as a boson.

A kaon decays into an antimuon and a neutrino, K⁺ →μ ⁺+v . The Feynman diagram for the decay is shown below.

(i) State the two particles labelled X and Y.

(ii) Explain how it can be deduced that this decay takes place through the weak interaction.

(iii) State the name and sign of the electric charge of the particle labelled A.

the spin number of a boson is an integer value;
the spin of the kaon can be \(\frac{1}{2} + \frac{1}{2} = 1\) or \(\frac{1}{2} - \frac{1}{2} = 0\)

(i) X: anti-strange quark / \(\bar s\);
Y: antimuon / μ⁺;

(ii) the process violates strangeness number conservation;
only the weak interaction allows this violation;

or

the decay of the kaon involves a neutrino;
any decay involving the neutrino must take place by the weak interaction;

(iii) name: W (boson);
sign: positive;

Identify the particles labelled A and B.

State, with reference to their properties, two differences between a photon and a W boson.

A: π⁺ meson;
B: antimuon neutrino;

rest mass is non-zero for W, zero for photon;
range of photon is infinite, not for W;
photon carries electromagnetic force, W weak force;
photon is uncharged, W is charged;

State the name of a particle that is its own antiparticle.

The meson K⁰ consists of a d quark and an anti s quark. The K⁰ decays into two pions as shown in the Feynman diagram.

(i) State a reason why the kaon K⁰ cannot be its own antiparticle.

(ii) Explain how it may be deduced that this decay is a weak interaction process.

photon / graviton / Z / Higgs;

(i) K⁰ has a strangeness of +1, its antiparticle has strangeness –1 and so are different;
the antiparticle is s, \(\overline d \) and so is different;

(ii) strangeness is violated in this decay;
this can only happen with the weak interaction;

(iii) Z⁰ / Z;

(iv) \(R = \left( {\frac{h}{{4\pi mc}} = } \right)\frac{{6.6 \times {{10}^{ - 34}}}}{{4 \times \pi  \times 1.6 \times {{10}^{ - 25}} \times 3.0 \times {{10}^8}}}\);
R≈10⁻¹⁸m;
Award [2] for a bald correct answer.

Deduce the strangeness of the Ω^– particle.

The Feynman diagram shows a quark change that gives rise to a possible decay of the Ω^– particle.

(i) Identify X.

(ii) Identify Y.

The number of lines per millimetre in the diffraction grating in (b) is reduced. Describe the effects of this change on the fringe pattern in (b).

-3;

(i) anti u (quark) /\(\bar u\);
(ii) W^–;

principal maxima broaden;

secondary maxima appear;

Deduce that the energy of a photon of wavelength 658 nm is 1.89 eV.

(i) On diagram 1, draw an arrow to show the electron transition between energy levels that gives rise to the emission of a photon of wavelength 658 nm. Label this arrow with the letter A.

(ii) On diagram 1, draw arrows to show the electron transitions between energy levels that give rise to the emission of photons of wavelengths 488 nm, 435 nm and 411 nm. Label these arrows with the letters B, C and D.

Explain why the lines in the emission spectrum of atomic hydrogen, shown in diagram 2, become closer together as the wavelength of the emitted photons decreases.

\(E = \frac{{hc}}{\lambda }\);
\( = \frac{{6.63 \times {{10}^{ - 34}} \times 3.00 \times {{10}^8}}}{{658 \times {{10}^{ - 9}}}} = 3.02 \times {10^{ - 19}}\);
=\(\frac{{3.02 \times {{10}^{ - 19}}}}{{1.60 \times {{10}^{ - 19}}}}\);
=1.89eV

or

the photon of wavelength 658nm is the longest (in the emission graph);
therefore it has the shortest frequency and lowest energy (from E=hf );
therefore it arises from the transition between the –1.51eV and the –3.40eV energy levels which have a difference of 1.89eV;

(i) see diagram below;

(ii) see diagram below;
All three must be correct for the mark.

at higher energy levels, energy levels become closer together;
the energy differences between higher energy levels and the lower level (n=2) become more equal;
hence the difference in wavelength of emitted photons decreases / OWTTE;

Determine the time taken for the foam to drop to

(i) half its initial height.

(ii) a quarter of its initial height.

The change in foam height can be modelled using ideas from other areas of physics. Identify one other situation in physics that is modelled in a similar way.

i

18 «s»

Allow answer in the range of 17 «s» to 19 «s».
Ignore wrong unit.

ii

36 «s»

Allow answer in the range of 35 «s» to 37 «s».

radioactive/nuclear decay
OR
capacitor discharge
OR
cooling

Accept any relevant situation, eg: critically damping, approaching terminal velocity

Outline how interactions in particle physics are understood in terms of exchange particles.

Determine whether or not strangeness is conserved in this decay.

The total energy of the particle represented by the dotted line is 1.2 GeV more than what is allowed by energy conservation. Determine the time interval from the emission of the particle from the s quark to its conversion into the d \({\rm{\bar d}}\) pair.

The pion is unstable and decays through the weak interaction into a neutrino and an anti-muon.

Draw a Feynman diagram for the decay of the pion, labelling all particles in the diagram.

exchange particles are virtual particles/bosons;
that mediate/carry/transmit the weak/strong/em force between interacting particles / OWTTE;
Award first marking point for named bosons also, e.g. photons, W, Z, gluons.

strangeness in initial state is –1 and zero in the final;
hence it is not conserved;

Award [0] for unsupported second marking point.

\(\Delta t \approx \frac{h}{{4\pi \Delta E}} = \frac{{6.63 \times {{10}^{ - 34}}}}{{4\pi  \times 1.2 \times {{10}^9} \times 1.6 \times {{10}^{ - 19}}}}\);
\(\Delta t \approx 3 \times {10^{ - 25}}{\rm{s}}\);

diagram as above;
correctly labelled W⁺;

Allow time to run vertically. Allow particle symbols. Ignore missing or wrong arrow directions.

Identify particle A.

(i) Identify the interaction whose exchange particle is represented by B.

(ii) Identify the exchange particle labelled C.

Outline how the concept of strangeness applies to the decay of a K⁺ meson shown in this Feynman diagram.

\(\pi \)^- / antiparticle of \(\pi \)⁺

Do not award mark if sign is omitted.

(i) (electro) weak;

(ii) gluon/photon;

strangeness is not conserved (in interaction B therefore it is a weak interaction);
strangeness is conserved in interaction C/in strong and electromagnetic interactions;

The Σ⁺ particle can decay into a π⁰ particle and another particle Y as shown in the Feynman diagram.

(i) Identify the exchange particle X.

(ii) Identify particle Y.

(iii) Outline the nature of the π⁰.

The π⁰ particle can decay with the emission of two gamma rays, each one of which can subsequently produce an electron and a positron.

(i) State the process by which the electron and the positron are produced.

(ii) Sketch the Feynman diagram for the process in (c)(i).

Discuss whether strangeness is conserved in the decay of the Σ⁺ particle in (a).

(i) W ^-; (allow W⁺,W boson)

(ii) proton;

(iii) π⁰ is a (neutral) meson;
π⁰ has integer spin/is a boson;
π⁰ is unstable;
π⁰ is its own antiparticle;

(i) pair production;

(ii)

single vertex showing photon and two correctly labelled particles;
arrow direction correct for e⁺ and e^-;
Allow time axis to run vertically.
If Feynman diagrams include the meson decay, only consider either gamma’s pair production.

strangeness is not conserved, changes from –1 to 0;
weak interaction does not have to conserve strangeness in decay of Σ⁺;
To award the mark reasoned answers are required.

An electron is excited to the n=3 energy level. On the diagram, draw arrows to show the possible electron transitions that can lead to the emission of a photon.

Show that a photon of wavelength 656 nm can be emitted from a hydrogen atom.

energy of photon is \(E = \left( {\frac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{656 \times {{10}^{ - 9}}}} = } \right)3.03 \times {10^{ - 19}}\left( {\rm{J}} \right)\);

Draw a Feynman diagram for this interaction.

Outline, with reference to the strong interaction, why hadrons are produced in the reaction.

State the reaction for the decay of the I-124 nuclide.

The graph below shows how the activity of a sample of iodine-124 changes with time.

(i) State the half-life of iodine-124.

(ii) Calculate the activity of the sample at 21 days.

(iii) A sample of an unknown radioisotope has a half-life twice that of iodine-124 and the same initial activity as the sample of iodine-124. On the axes opposite, draw a graph to show how the activity of the sample would change with time. Label this graph X.

(iv) A second sample of iodine-124 has half the initial activity as the original sample of iodine-124. On the axes opposite, draw a graph to show how the activity of this sample would change with time. Label this graph Y.

\({}_{53}^{124}{\rm{I}} \to {}_{52}^{124}{\rm{Te + }}{}_1^0\beta ^+ \);
\({}_0^0v/v\);
Do not allow an antineutrino.
Award [1 max] for \({}_{53}^{124}{\rm{I}} \to {}_{54}^{124}{\rm{Te + }}{}_1^0\beta^-  + \bar v\).

(i) 4 days;

(ii) \(\lambda  = \frac{{\ln 2}}{{{T_{\frac{1}{2}}}}} = \frac{{\ln 2}}{4} = \left( {0.173{\rm{da}}{{\rm{y}}^{ - 1}}} \right)\);
\(A = {A_0}{e^{ - \lambda t}} = 16 \times {10^7} \times {e^{ - 0.173 \times 21}}\left( {{\rm{Bq}}} \right)\);
A=4.2×10⁶Bq; 
Award [2 max] for bald answer in range 4.2−4.5×10⁶ Bq, or linear interpolation between half lives giving 4.4×10⁶Bq.

(iii) graph passing through or near (0,16), (8,8) and (16,4) – see below;

(iv) graph passing through or near (0,8), (4,4) and (8,2) – see below; 
Do not penalize if graph does not pass through (12,1) and (16,0.5).

Explain how atomic spectra provide evidence for the quantization of energy in atoms.

Outline how the de Broglie hypothesis explains the existence of a discrete set of wavefunctions for electrons confined in a box of length L.

The diagram below shows the shape of two allowed wavefunctions ѱ_A and ѱ_B for an electron confined in a one-dimensional box of length L.

(i) With reference to the de Broglie hypothesis, suggest which wavefunction corresponds to the larger electron energy.

(ii) Predict and explain which wavefunction indicates a larger probability of finding the electron near the position \(\frac{L}{2}\) in the box.

(iii) On the graph in (c) on page 7, sketch a possible wavefunction for the lowest energy state of the electron.

atomic spectra have discrete line structures / only discrete frequencies/wavelengths;
photon energy is related to frequency/wavelength;
photons have discrete energies;
photons arise from electron transitions between energy levels;
which must have discrete values of energy;

de Broglie suggests that electrons/all particles have an associated wavelength; this wave will be a stationary wave which meets the boundary conditions of the box; the stationary wave has wavelength \(\frac{{2L}}{n}\) (where L is the length of the box and where n is an integer);

(i) wavelength of ψ_A larger than ψ_B;
therefore momentum of ψ_B larger than ψ_A (from de Broglie hypothesis); therefore ψ_B has larger energy;
Award [1 max] for a bald correct answer.

or

ψ_B has n=3, ψ_A has n=2;
E_K ∝ n²;
so ψ_B corresponds to the larger energy;

(ii) ψ_A=0, ψ_B≠0 in the middle of the box/at \(\frac{L}{2}\);
so ψ_B corresponds to the larger probability since probability ∝ΙψΙ²;
Accept ∝ ψ².

or

the probability (of finding the electron) is related to the amplitude;
amplitude of ψ_B is greater than amplitude of ψ_A so ψ_B is more likely to be found;

Award [1 max] for a bald correct answer.

(iii)

correct sketch; (accept -ψ)
Accept wavefunction with any amplitude.